How to Make a Circle Using the Shapely Library in Python

When working with geospatial data in Python, you might find yourself needing to create a perfectly round circle. The Shapely library is a popular tool for this task, but it’s not always as straightforward as it seems. Here is given code to create circle using Shapely library in python.

The Shapely’s Buffer Function Dilemma

You might think that Shapely’s buffer function would be the go-to method for creating a circle. However, there’s a significant issue with this approach. When you use the buffer function, it doesn’t create a perfect circle. Instead, it creates an ellipse shape, which might not be suitable for your needs.

This discrepancy occurs because the buffer function doesn’t account for the curvature of the Earth, leading to an elliptical shape rather than a round one.

A Perfect Solution: Geodesic Point Buffer

To create perfectly round circle, you will need shapely and pyproj libraries. Which you can install by the below commands:

• pip install shapely
• pip install pyproj

from pyproj import CRS, Transformer
from shapely.geometry import Point
from shapely.geometry import Polygon
from shapely.ops import transform

def geodesic_point_buffer(lat, lon, radius):
    """
    Creates circles from given latitude, longitude, and radius

    :param lat: latitude from original data
    :param lon: longitude from original data
    :param radius: radius from original data
    """
    # Azimuthal equidistant projection
    aeqd_proj = CRS.from_proj4(f"+proj=aeqd +lat_0={lat} +lon_0={lon} +x_0=0 +y_0=0")
    tfmr = Transformer.from_proj(aeqd_proj, aeqd_proj.geodetic_crs)
    buf = Point(0, 0).buffer(radius * 1609.34)  # distance in miles
    return Polygon(transform(tfmr.transform, buf).exterior.coords[:])

Understanding the Function

This function takes three parameters: latitude (lat), longitude (lon), and radius (radius). Here’s how it works:

1. Azimuthal Equidistant Projection: This projection ensures that distances from the center (latitude and longitude) to any point on the map are accurate. It’s defined using the CRS.from_proj4 method.
2. Transformation: The Transformer.from_proj method is used to create a transformation between the azimuthal equidistant projection and the geodetic coordinate reference system.
3. Buffer Creation: The Point(0, 0).buffer(radius * 1609.34) part creates a buffer around the point (0,0) with the specified radius, converting it to miles.
4. Polygon Transformation: Finally, the Polygon object is created by transforming the buffer using the previously defined transformer. The result is a perfectly round circle.

Bonus: Visualise created circle

When you have created the circle by using the above function, you would want to check how the circle is visually on the map for sanity checking and other reasons. And why not?As a solution to this, there is one site called Kepler.gl will help you.

On this site, you have to upload your CSV with polygon values of circles and that’s it. Kepler.gl will do the rest of the things and it will show you the resultant polygons(In our case they are in the circle) very nicely. Below is an example from one of the files.

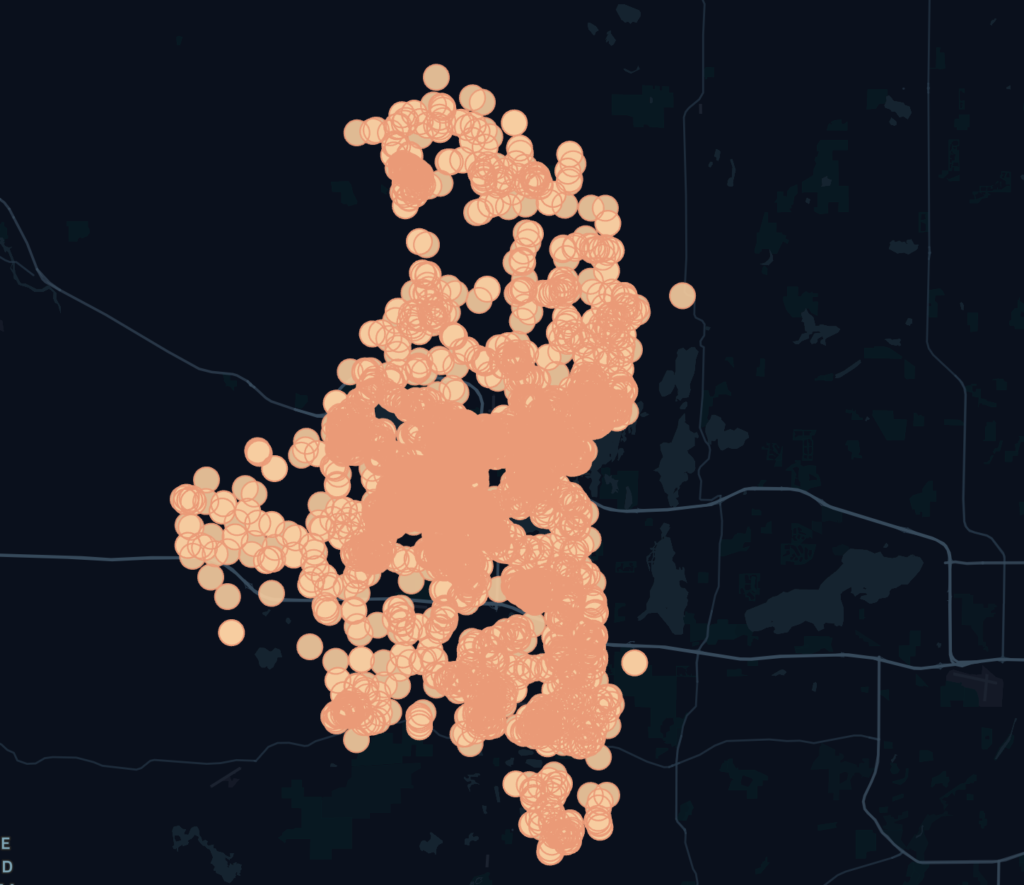
Conclusion

Creating a perfect circle in geospatial data processing can be a tricky task. While Shapely’s buffer function might seem like the obvious choice, it falls short by creating an ellipse instead of a circle. The geodesic_point_buffer function provides a robust solution, taking into account the Earth’s curvature to generate a perfectly round shape.

By understanding the underlying principles and utilizing the provided function, you can create accurate and visually appealing circles for your geospatial projects. Whether you’re mapping a specific area or visualizing data, this method ensures precision and consistency in your work. Happy coding!

Also read: Easy way to calculate the standard deviation or variance of the tensor in TensorFlow?